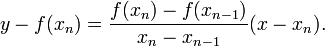Metodo de sekigita
fonto: http://pt.wikipedia.org/wiki/M%C3%A9todo_das_secantes
En cifereca analitiko , la metodo de sekigita estas serĉo algoritmo kiu uzas radikon vico de radikoj de sekanto liniojn al aproksimi pli kaj pli la radiko de funkcio f.
La metodo de sekigita estas difinita de la rekursieca rilato
Ĉi tiu rezulto estas valida nur sub certaj teknikaj kondiĉoj, nome f esti dufoje kontinue diferencialebla kaj la radiko en demando devus esti simpla (te, ne devus esti oblo radiko).
Se la komenca valoroj ne estas proksime de la radiko, ne estas garantio, ke la metodo de sekigita konverĝas.
La metodo
Derivaĵo de la metodo
Datumoj x n kaj x n -1, ni konstruis linion pasante tra la punktoj (x n -1, f (x n-1)) kaj (x n, f (x n)), kiel ilustrita en la dekstra figuro. Notu ke ĉi linio estas sekanto aŭ akordo de la grafeo de la funkcio f. En punkto-inklina formo, ĝi povas esti difinita kielKonverĝo
X n iteraciones de la metodo de sekigita konverĝi al radiko de f, se la komencaj valoroj x 0 kaj x 1 estas sufiĉe proksima al la radiko. La ordo de konverĝo de la metodo estas α, kieĈi tiu rezulto estas valida nur sub certaj teknikaj kondiĉoj, nome f esti dufoje kontinue diferencialebla kaj la radiko en demando devus esti simpla (te, ne devus esti oblo radiko).
Se la komenca valoroj ne estas proksime de la radiko, ne estas garantio, ke la metodo de sekigita konverĝas.